Telescope Making
Equations for Pointing Telescope
Written by Toshimi Taki
Revision A: January 12, 2002
Revision B: April 3, 2004
Introduction
My report titled "A New Concept in Computer-Aided Telescopes" was published in February 1989 issue of Sky & Telescope Magazine. I presented a new algorithm to aim a telescope in the article. You can download the BASIC program, TAKI.BAS from
Sky Publishing Home Page.
------------------------ NOTE -------------------------
I found errors in TAKI.BAS recently. Please make the following
corrections in the BASIC program.
Wrong: 760 Y(1,0)=Y(1,0)+SIN(F)*COS(H)*(Z1/G)
Correct: 760 Y(1,0)=Y(1,0)+SIN(F)*SIN(H)*(Z1/G)
Wrong: 795 Y(1,1)=Y(1,1)-SIN(F)*COS(H)*(Z1/G)
Correct: 795 Y(1,1)=Y(1,1)-SIN(F)*SIN(H)*(Z1/G)
--------------------------------------------------------
Palm Pilot version is developed by David Ditch and you can download it from
his website.
Since then, the algorism has been widely used by amateurs and some of the advanced amateurs are using the algorism to control Dobsonian telescopes. Mel Bartel has developed such kind of control system and he presents his software in
his home page.
Because of the limited space of the magazine, the detailed equations behind the algorithm were omitted. So I would like to present all the detailed equations here. I also present a software to find mount error. I hope this will be helpful to understand the algorithm.
If you interested in the matrix method which I used to develop the equations, see
"Matrix Method for Coordinates Transformation" in my home page.
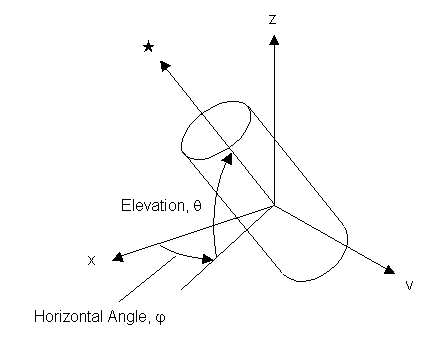
Definition of Coordinate Systems
The telescope coordinate system is defined as shown in figure 1. The position of a star will be specified in horizontal angle,
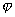 and elevation,
and elevation,
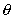 .
The telescope is not necessarily leveled or aligned with any directions. Note that the horizontal angle is measured right to left. This is the opposite direction to azimuth.
.
The telescope is not necessarily leveled or aligned with any directions. Note that the horizontal angle is measured right to left. This is the opposite direction to azimuth.
 .
.
Figure 1. Definition of Telescope Coordinate System
Equations for Perfect Mount
First, equations for perfect mount are presented.
The relationship between telescope coordinate and equatorial coordinate is expressed as follows using direction cosines of both coordinates.
Transformation from equatorial coordinate to telescope coordinate,
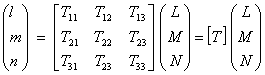 .... equation (1)
.... equation (1)
Transformation from telescope coordinate to equatorial coodinate,
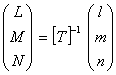 .... equation (2)
.... equation (2)
Where,
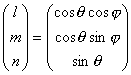 : Direction cosine of an object in telescope coordinate system .... equation (3)
: Direction cosine of an object in telescope coordinate system .... equation (3)
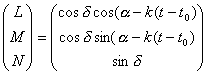 : Direction cosine of an object in equatorial coordinate system .... equation (4)
: Direction cosine of an object in equatorial coordinate system .... equation (4)
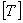 ,
,
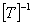 : Transformation matrix and its inverse matrix
: Transformation matrix and its inverse matrix
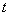 : Time
: Time
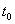 : Initial time
: Initial time
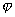 : Horizontal angle of an object
: Horizontal angle of an object
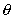 : Elevation of an object
: Elevation of an object
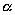 : Right Ascension of an object
: Right Ascension of an object
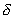 : Declination of an object
: Declination of an object
Transformation Matrix
Transformation matrix can be determined by using 2 reference stars.
For reference star 1
Observed time :
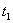
Telescope coordinate :
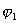 ,
,
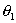
Equatorial coordinate :
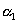 ,
,
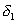
For reference star 2
Observed time :
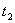
Telescope coordinate :
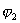 ,
,
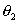
Equatorial coordinate :
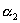 ,
,
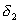
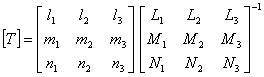 .... equation (5)
.... equation (5)
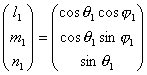 .... equation (6)
.... equation (6)
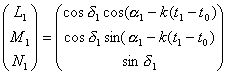 .... equation (7)
.... equation (7)
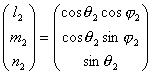 .... equation (8)
.... equation (8)
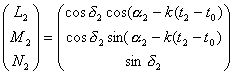 .... equation (9)
.... equation (9)
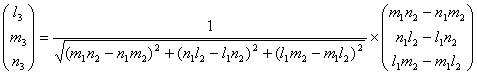 .... equation (10)
.... equation (10)
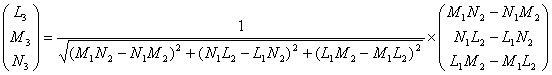 .... equation (11)
.... equation (11)
Equations for Mount with Fabrication Error
All telescope mounts have fabrication error in the real world, especially for home built telescopes. In this section, equations for mount with fabrication error are presented. See figure 2 for the definition of mount error angles.
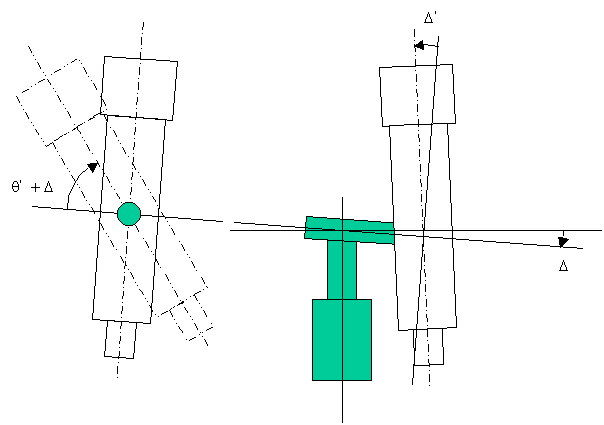
Figure 2. Definition of Telescope Mount Error
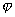 : True horizontal angle
: True horizontal angle
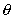 : True elevation
: True elevation
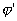 : Apparent horizontal angle
: Apparent horizontal angle
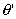 : Apparent elevation
: Apparent elevation
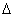 : Mount error angle between horizontal axis and vertical axis
: Mount error angle between horizontal axis and vertical axis
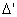 : Mount error angle between vertical axis and telescope optical axis
: Mount error angle between vertical axis and telescope optical axis
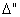 : Mount error angle, zero point shift
: Mount error angle, zero point shift
The direction cosine of true telescope angles can be expressed using apparent telescope angles as follows.

.... equation (12)
Since mount error angles, 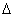 and
and 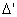 are very small, we can use the following approximation. Note that
are very small, we can use the following approximation. Note that 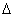 and
and 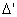 are in radian.
are in radian.
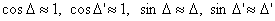
Equation (12) is simplified as follows.
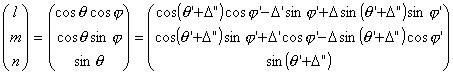 .... equation (13)
.... equation (13)
Again, mount error angles, 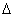 and
and 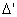 are very small, we can use the following approximation.
are very small, we can use the following approximation.
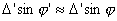 ,
,
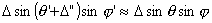 ,
,
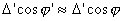 ,
,
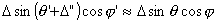
Apparent telescope angles can be calculated from true telescope angles as follows.
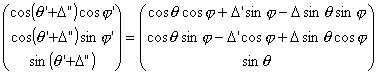 .... equation (14)
.... equation (14)
Procedure of Calculation
1. Initialization
(1) Point your telescope to two known stars (call them reference stars) and measure the apparent telescope angles.
(2) Using equation (12), calcuate direction cosines of true telescope angles for the 2 reference stars.
(3) Using equations (7) and (9), calculate direction cosines of equatorial coordinates for the 2 reference stars.
(4) Using equations (10) and (11), calculate the additional directions cosines.
(5) Apply equation (5) and calculate the transformation matrix, [T]. Note that the transformation matrix is for the direction cosine of true telescope angles.
2. Point your telescope to known object
(1) Using equations (4) and (1) with equatorial coordinate of a known object, calculate direction cosine of true telescope angles of the object. Then, apply equation (14) to find direction cosine of apparent telescope angles of the object. The apparent angles is calculated from the direction cosine.
(2) Point your telescope to the apparent angle and you will find the object in the field of your telecope.
3. Find equatorial coordinate of unknown object
(1) Measure apparent telescope angle of unknown object and record the observed time.
(2) Calculate direction cosine of the true telescope angles using equation (12).
(3) Calculate direction cosine of equatorial coordinate using equation (2). Then, equatorial coordinate of the unknown object is calculated using equation (4).
Finding Fabrication Error of Mount
I developed MS-Excel 2000 worksheet to find fabrication error of mount. You can download the file, "mount_error_b.xls" here.
Click here to download "mount_error_b.xls".
Reference
[1] Toshimi Taki, "A New Concept in Computer-Aided Telescopes," Sky & Telescope, February 1989, pp.194-196.
[2] Toshimi Taki, "New Method for Pointing of Alt-azimuth Mount Telescope," Hoshi-no-Techo, Volume 35, 1987, pp.94-97. (in Japanese)
[3] Toshimi Taki, "Improvement of Pointing Method of Alt-azimuth Mount Telescope," Hoshi-no-Techo, Volume 39, 1988, pp.94-100. (in Japanese)
==========================================================
Revision History
Revision A (January 12, 2002)
- Eorrors in equations (12) to (14) are corrected.
- "mount_error.xls" is revised using coorected equations.
Revision B (April 3, 2004)
- "mount_error_b.xls" is revised.
 Return to Home
Return to Home
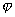 and elevation,
and elevation,
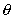 .
The telescope is not necessarily leveled or aligned with any directions. Note that the horizontal angle is measured right to left. This is the opposite direction to azimuth.
.
The telescope is not necessarily leveled or aligned with any directions. Note that the horizontal angle is measured right to left. This is the opposite direction to azimuth.
 .
.
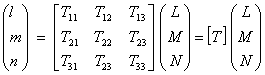 .... equation (1)
.... equation (1)
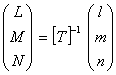 .... equation (2)
.... equation (2)
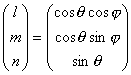 : Direction cosine of an object in telescope coordinate system .... equation (3)
: Direction cosine of an object in telescope coordinate system .... equation (3)
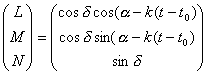 : Direction cosine of an object in equatorial coordinate system .... equation (4)
: Direction cosine of an object in equatorial coordinate system .... equation (4)
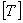 ,
,
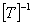 : Transformation matrix and its inverse matrix
: Transformation matrix and its inverse matrix
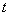 : Time
: Time
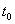 : Initial time
: Initial time
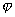 : Horizontal angle of an object
: Horizontal angle of an object
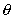 : Elevation of an object
: Elevation of an object
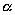 : Right Ascension of an object
: Right Ascension of an object
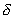 : Declination of an object
: Declination of an object
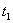
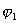 ,
,
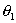
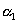 ,
,
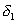
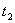
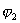 ,
,
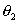
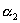 ,
,
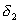
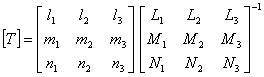 .... equation (5)
.... equation (5)
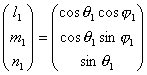 .... equation (6)
.... equation (6)
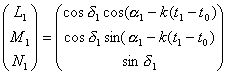 .... equation (7)
.... equation (7)
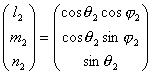 .... equation (8)
.... equation (8)
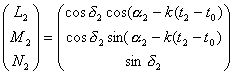 .... equation (9)
.... equation (9)
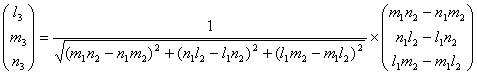 .... equation (10)
.... equation (10)
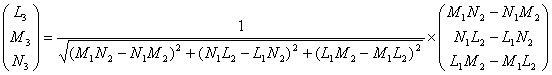 .... equation (11)
.... equation (11)

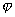 : True horizontal angle
: True horizontal angle
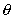 : True elevation
: True elevation
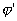 : Apparent horizontal angle
: Apparent horizontal angle
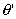 : Apparent elevation
: Apparent elevation
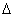 : Mount error angle between horizontal axis and vertical axis
: Mount error angle between horizontal axis and vertical axis
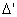 : Mount error angle between vertical axis and telescope optical axis
: Mount error angle between vertical axis and telescope optical axis
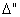 : Mount error angle, zero point shift
: Mount error angle, zero point shift

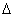 and
and 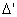 are very small, we can use the following approximation. Note that
are very small, we can use the following approximation. Note that 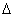 and
and 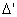 are in radian.
are in radian.
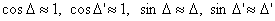
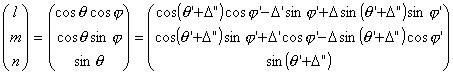 .... equation (13)
.... equation (13)
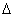 and
and 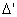 are very small, we can use the following approximation.
are very small, we can use the following approximation.
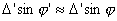 ,
,
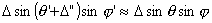 ,
,
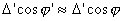 ,
,
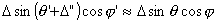
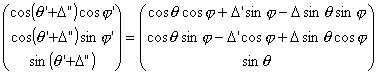 .... equation (14)
.... equation (14)